Hello my dear friends. Today, we’ll talk about storing tree structures in the RDBMS (Relational Database Management Systems: e.g. MySQL, PostgreSQL, Oracle, etc.).
While this can be an easy topic for some of you (if “Nested Sets” and “Materialized Path” sound familiar, you probably won’t find anything new here), I’ve decided to post this article due to a number of discussions on storing tree structures in RDBMS after the PostgreSQL conferences where I was a speaker. It came as a surprise to me that a lot of people know merely about “parent-child” pattern for storing tree structures, and in this article I would like elaborate on this and other patterns more. Also, while building some complex systems, you need to consider using relational database and may decide to evaluate other options, like Neo4j or FlockDB.
Parent-child
This is the most common and simple pattern for storing trees. Numerous implementations of it can be found in forum systems, commenting systems, etc. The essence of this pattern is described on the picture below: each element holds a reference (ID) to the parent as a foreign key (on the picture, PK – primary key, FK – foreign key). This is a typical one-to-many relationship.
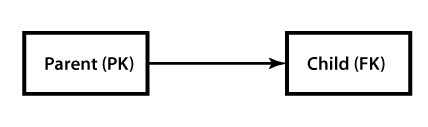
Adding and Editing
Adding and changing elements in the tree is a piece of cake – just specify the parent ID and you’re done.
Removal
Removal is a bit more difficult though. If you simply delete an item, there will be a problem with lost children. Therefore, you need to keep track of the application and implement logic to remove children of this specific item. Typical solution here is not to delete this item, but mark it as deleted and transfer to the direct descendant and then to their direct descendants and so on. In this casem all your descendants (direct and indirect – i.e., grandchildren) of the root will be marked as deleted.
Selection
This is the most problematic area of the pattern as there’s not much possibility for performing a simple selection. In a nutshell, this pattern allows you to choose only all the direct descendants of the item. Functions like selecting all the descendants – direct and indirect – building the path from the root (the choice of all parents), as well as recursive function are implemented in the application or multiple JOINs.
The number of elements and levels of nesting
Number of elements and levels of nesting is virtually endless and does not depend on the dimension of the field ID.
Summary
If you go with this pattern, adding and moving items will be really simple. It is also very efficient when there’s a need for frequent structure changes (data is added often, multiple uploads). But there’s also a price for this simplicity, and often – a significant one. In this case, you’ll have to sacrifice performance when you fetch data.
Materialized Path
Despite the terrible name, this is a very common pattern that is also the closest one to the common human logic. Without knowing its name, we encounter this pattern all the time: e.g. library lists, URL in a browser and even the Bible. The essence of this pattern is that the each element stores the full path from the very root. For example, “Part 22, Section 8, Chapter 21, paragraph 2”.
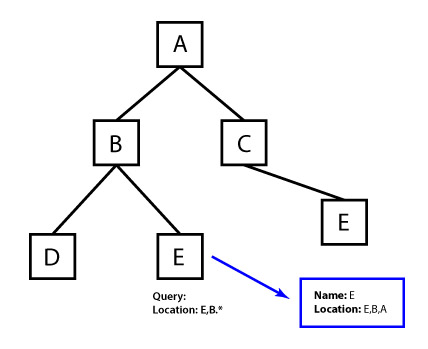
Adding and Editing
It’s a bit more difficult here than in the “Parent-child” pattern. To add an item, you should get parent’s path (ID) and add to it your ID. It gets more complicated with changing an item though. In this case, you should recalculate ID (actually – calculate the way) of all the children, both direct and indirect.
Removal
Removing an item is more interesting. Simple removal of any element doesn’t violate the tree integrity. Descendants of the deleted item are still indirect descendants of the remote parent. Children of dead parents aren’t orphans, they have grandparents :)
Selection
This is the forte of this pattern. To be able to select with simple queries you can use various options which would have caused a lot of headache with the “parent-child” pattern. ID of all parents (full path) from the root isn’t a problem at all. For example, you can select all direct and indirect descendants using this SQL: “SELECT * FROM … WHERE ID LIKE ‘00010001% ‘”. This pattern is very convenient to use for the construction in various directories – such as a request “the first three sections with the largest number of elements, including nested”. It is very easy and does not require lots of recursive calls.
The number of elements and levels of nesting
Design of these parameters is entirely up to a developer. In fact, often there’s no need for the infinite number of levels: if sections nesting on the web site gets close to 20, perhaps you should think about re-developing the site, rather than increasing levels. There could be different implementations of the method. Data type in field in the ID-way can be bit or text. A text box can contain elements separated by character such as a point (1.1.2.5) or a backslash (‘\test\chapter\hello’). Quite often, a fixed number of characters is being used for each level, supplemented by, for example, zeros (0001000100020005 – a fourth level of 4 characters each). This makes it easy to determine the length of the line level, get the parent ID, etc. Besides, who says that only numbers can be used for numbering? If we add them to the Latin alphabet chart, we will get numbers in the 36-hexadecimal number (10 digits + 26 letters).
Summary
This pattern can be used for frequent selections and additions with minimal structural changes. While doing a thorough planning of the system’s identifier, it is impossible to apply the auto-increment field, i.e. ID formation rests on the shoulders of the programmer. ID type VARCHAR (255) is also not encouraging – especially for the fans of semantics – because the text box, horror of horrors, stores not only the text data.
Nested Sets
This pattern is a bit more difficult to understand. The idea itself is similar to the previous pattern – simplify selection of children. Unlike “Materialized Path”, however, item here does not store explicit path information. But let’s consider the pattern based on the element ID. Not only your place stores this item, but also ID neighbours on the same level. If a neighbour is not on the same level, then the ID of the level above is stored. In the picture below, item 1 knows that his neighbor “to the left” – 0, “right” – 14. How many elements a child element “Vegetable” has? (7 – 2 – 1) / 2 = 2 (“Potato” and “Tomato”). What are the parents of the “Tomato” element? All elements with “neighbours left” less than 5 (ID) and the “right-hand man” for more than 6 (ID). “Vegetable” and “Food” fall under the request. All this is a a bit unreadable. “Left” and “right” to receive “top” and “bottom” – not for people that are used to think in rows of tables.
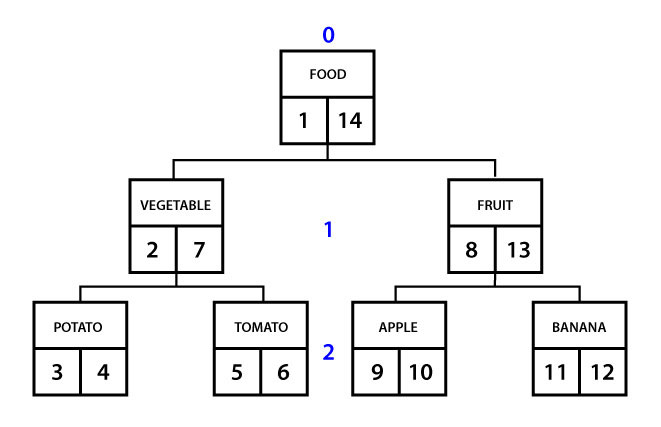
Adding and Editing
This is an extremely complex procedure that requires recalculation of the ID, neighbours’ numbers, and restating of the corresponding fields from neighbors and parents. An average conversion will affect half (sic!) of records in a table.
Removal
Removing, in theory, is a complex procedure too, as it also requires recalculation of borders and ID. However, it is possible to delay and run background job, or do it on schedule. Simply removing an element does not mean entire loss of a tree of children elements, they also fall within the boundaries of the parents and the parents become subject parent. Thus, after removing element 6, elements 7 and 8 will belong to the element 3.
Selection
This is what all these bells and whistles are for. As described above, ID subsidiaries – direct and indirect – of elements (and numbers) can be calculated easily, without using the database. Provided, of course, that the elements are properly disposed of, with the conversion boundaries. Well, ID elements must be integers. Construction path to the root is built as described above.
The number of elements and levels of nesting
This is a strength of the pattern. The number of elements and levels of nesting, as in the “parent-child” pattern depends on the implementation of integer fields in the database and isn’t allowed to be designed. Well, up to certain limits, of course.
Summary
This pattern is suitable for frequent selections and rare additions or changes. Restriction on nesting does not require preliminary calculations. It is suitable for various directories, e.g. product catalogs. There is an interesting modification of this method which is based on the fact that ID can’t be an integer and boundaries do not touch each other. All in all, my picture should help you realize the item has one “right” (bottom) of the # 3 and 2.3 (two point three) and we still have a place for painless insertion elements. The main requirement is to calculate the boundary element that would be added to the “gap”, i.e. inserting the component between 1 and 3, to install it, and the left border 2.4 2.8. Right, i.e. always keep a free interval. While using this method you can get your item with ID infinitesimal.
Summary
Of course, these are only the most common solutions, and for sure there are techniques that I don’t know. Relational databases (RDBMS) are generally not very well suited for storing tree structures, but that’s another topic. We should choose carefully what pattern to use because each of them has certain disadvantages. The good news is that there are plenty to choose from.
That’s all folks! Thanks for reading till the very end.
This is a re-post from my blog.
