Hello my dear friends. In “
PostgreSQL most useful extensions” I showed a list of some useful extensions for PostgreSQL. Of course, that article didn’t cover all useful extensions (in my humble opinion) and some extensions I want to describe in separate articles. Today we will talk about effective similarity search in PostgreSQL.Similarity search in large databases is an important issue in nowadays informational services, such as recommender systems, blogs (similar articles), online shops (similar products), image hosting services (similar images, search image duplicates) etc. PostgreSQL allows to make such things more easy. First you need to understand how we will calculate the similarity of two objects.
Similarity
Any object can be described by a list of characteristics. For example, article in blog can be described by tags, product in online shop – by size, weight, color etc. It means that for each object we can create the digital signature – array of numbers, which describing the object (
fingerprint,
n-grams). Let’s create an array of not ordered numbers for every object. What should we do next?
Similarity calculation
There are several methods for calculating the similarity of objects by signatures. First of all, the legend for calculations:Na, Nb – the number of unique elements in the arraysNu – the number of unique elements in the union of setsNi – the number of unique elements in the intersection of arraysOne of the simplest calculation of the similarity of two objects is the number of unique elements in the intersection of arrays divided by the number of unique elements in two arrays:
%20=%20frac%7BN_%7Bi%7D%7D%7B(N_%7Ba%7D%20+%20N_%7Bb%7D)%7D)
or only
%20=%20frac%7BN_%7Bi%7D%7D%7BN_%7Bu%7D%7D)
Pros:
- Easy to understand
- Speed of calculation: N * log(N)
- Works well at similar and large Na and Nb
Similarity can also be calculated using the formula of cosines:
%20=%20frac%7BN_%7Bi%7D%7D%7Bsqrt%7BN_%7Ba%7D%20*%20N_%7Bb%7D%7D%7D)
Pros:
- Speed of calculation: N * log(N)
- Works well for large N
But both of these metrics have common problems:
- Few elements -> large scatter of similarity
- Frequent elements -> weight below
TF/IDF metric avoids these problems to calculate the similarity:
%20=%20frac%7Bsum_%7Bi%20%3C%20N_%7Ba%7D,%20j%20%3C%20N_%7Bb%7D,%20A_%7Bi%7D%20=%20B_%7Bj%7D%7DTF_%7Bi%7D%20*%20TF_%7Bj%7D%7D%7Bsqrt%7Bsum_%7Bi%20%3C%20N_%7Ba%7D%7DTF_%7Bi%7D%5E%7B2%7D%20*%20sum_%7Bj%20%3C%20N_%7Bb%7D%7DTF_%7Bj%7D%5E%7B2%7D%7D%7D)
where
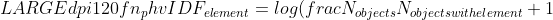)
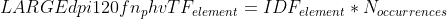
Now it would be great to use this knowledge in practice.
Smlar extension for PostgreSQL
Oleg Bartunov and Teodor Sigaev developed PostgreSQL extension, called smlar, which provides several methods to calculate sets similarity (all built-in data types supported), similarity operator with indexing support on the base of GiST and GIN frameworks. Let’s look how to work with this extension. First of all, we need install it (PostgreSQL should be already installed):
git clone git://sigaev.ru/smlar
cd smlar
USE_PGXS=1 make && make install
On PostgreSQL 9.2 this extension should build without problem, for PostgreSQL 9.1 and earlier you need to make a little fix. In file “smlar_guc.c” on line 214 change call
set_config_option("smlar.threshold", buf,
PGC_USERSET, PGC_S_SESSION ,GUC_ACTION_SET, true, 0);
to this (delete last argument)
set_config_option("smlar.threshold", buf,
PGC_USERSET, PGC_S_SESSION ,GUC_ACTION_SET, true);
Let’s test instaled extension:
$ psql -d test
psql (9.1.3)
Type "help" for help.
test=# CREATE EXTENSION smlar;
CREATE EXTENSION
test=# SELECT smlar('{1,4,6}'::int[], '{5,4,6}' );
smlar
----------
0.666667
(1 row)
test=# SELECT smlar('{1,4,6}'::int[], '{5,4,6}', 'N.i / sqrt(N.a * N.b)' );
smlar
----------
0.666667
(1 row)
If you have the same output in console, you’ve installed extension successful. More information about this extension you can read in README file.Function smlar computes similary of two arrays (arrays should be the same type) and return float from 0 to 1 (0 – absolutely no similar objects, 1 – absolutely similar arrays, equal). Function can take the third argument – the formula, that calculates the similarity of the two arrays. Module provides several GUC variables and it’s highly recommended to add to postgesql.conf:
custom_variable_classes = 'smlar' # list of custom variable class names
smlar.threshold = 0.8 # or any other value > 0 and < 1
Array’s with similarity lower than ‘smlar.threshold’ are not similar by % operation.
test=# SELECT '{1,4,6,5,7,9}'::int[] % '{1,5,4,6,7,8,9}'::int[] as similar;
similar
---------
t
(1 row)
GiST/GIN support for % operation. The parameter “similar.type” allows you to specify what kind of formula used to calculate the similarity: cosine (default), overlap or tfidf. For “tfidf” need to make additional configuration, but I will not consider this in the article (all can be found in the README file). Now let’s consider an example of using this extension.
Finding duplicate of images
For example, I select the search for duplicate images. Other options for shopping, blogs are implemented in a similar way. The algorithm helps to find similar images that are slightly different: desaturated images, add watermark, passed through the filters.In our algorithm, we will create a pixel matrix of each image. Let it be 15×15 pixels. The next step: we do not know the color of a pixel, but its intensity (the intensity is given by 0.299 * red + 0,587 * green + 0,114 * blue). Calculating the intensity will help us find the image is not paying attention to the colors of the images.

Once you have to calculate the intensity of all pixels in a 15×15 matrix, we find the ratio of the intensity of each pixel to the mean intensity of the matrix, and generate a unique number for each cell (in the code to generate unique for each cell, I added the coordinates to intensity) and obtain an array of 225 elements length (15 * 15 = 225). Excellent.
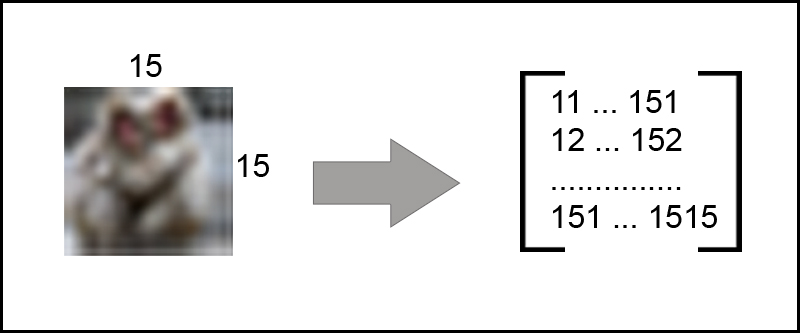
Below is the code to generate a digital signature for images on Ruby and PHP languages:
Ruby PHP  |  |
| 61,33% similarity |
 |  |
| 23,56% similarity |
 |  |
| 87,55% similarity |
Excellent, but it is comparing two images. Now let’s use PostgreSQL for searching. In PostgreSQL is an array type of the field. We will write the digital signature of the image:
CREATE TABLE images (
id serial PRIMARY KEY,
name varchar(50),
image_array integer[]
);
INSERT into images(image_array) VALUES ('{1010257,...,2424257}');
test=# SELECT count(*) from images;
count
--------
200000
(1 row)
test=# EXPLAIN ANALYZE SELECT id FROM images WHERE images.image_array % '{1010259,...,2424252}'::int[];
Aggregate (cost=14.58..14.59 rows=1 width=0) (actual time=1.785..1.785 rows=1 loops=1)
-> Seq Scan on images (cost=0.00..14.50 rows=33 width=0) (actual time=0.115..1.772 rows=20 loops=1)
Filter: (image_array % '{1010259,1011253,...,2423253,2424252}'::integer[])
Total runtime: 5152.819 ms
(4 rows)
It works, but search works without index. Let’s create it:
CREATE INDEX image_array_gin ON images USING GIN(image_array _int4_sml_ops);
or
CREATE INDEX image_array_gist ON images USING GIST(image_array _int4_sml_ops);
Difference between GiST and GIN indexes you can read
here.
test=# EXPLAIN ANALYZE SELECT id FROM images WHERE images.image_array % '{1010259,1011253,...,2423253,2424252}'::int[];
Aggregate (cost=815.75..815.76 rows=1 width=0) (actual time=320.428..320.428 rows=1 loops=1)
-> Bitmap Heap Scan on images (cost=66.42..815.25 rows=200 width=0) (actual time=108.127..304.524 rows=40000 loops=1)
Recheck Cond: (image_array % '{1010259,1011253,...,2424252}'::integer[])
-> Bitmap Index Scan on image_array_gist (cost=0.00..66.37 rows=200 width=0) (actual time=90.814..90.814 rows=40000 loops=1)
Index Cond: (image_array % '{1010259,1011253,...,2424252}'::integer[])
Total runtime: 320.487 ms
(6 rows)
Perfect! Let’s check performance.
test=# SELECT count(*) from images;
count
---------
1000000
(1 row)
test=# EXPLAIN ANALYZE SELECT count(*) FROM images WHERE images.image_array % '{1010259,1011253,...,2423253,2424252}'::int[];
Bitmap Heap Scan on images (cost=286.64..3969.45 rows=986 width=4) (actual time=504.312..2047.533 rows=200000 loops=1)
Recheck Cond: (image_array % '{1010259,1011253,...,2423253,2424252}'::integer[])
-> Bitmap Index Scan on image_array_gist (cost=0.00..286.39 rows=986 width=0) (actual time=446.109..446.109 rows=200000 loops=1)
Index Cond: (image_array % '{1010259,1011253,...,2423253,2424252}'::integer[])
Total runtime: 2152.411 ms
(5 rows)
Let’s add sorting in SQL (the most similar images were the first), and add similarity as extra field:
EXPLAIN ANALYZE SELECT smlar(images.image_array, '{1010259,...,2424252}'::int[]) as similarity FROM images WHERE images.image_array % '{1010259,1011253, ...,2423253,2424252}'::int[] ORDER BY similarity DESC;
Sort (cost=4020.94..4023.41 rows=986 width=924) (actual time=2888.472..2901.977 rows=200000 loops=1)
Sort Key: (smlar(image_array, '{...,2424252}'::integer[]))
Sort Method: quicksort Memory: 15520kB
-> Bitmap Heap Scan on images (cost=286.64..3971.91 rows=986 width=924) (actual time=474.436..2729.638 rows=200000 loops=1)
Recheck Cond: (image_array % '{...,2424252}'::integer[])
-> Bitmap Index Scan on image_array_gist (cost=0.00..286.39 rows=986 width=0) (actual time=421.140..421.140 rows=200000 loops=1)
Index Cond: (image_array % '{...,2424252}'::integer[])
Total runtime: 2912.207 ms
(8 rows)
Added sorting did not complicate query execution.
Here you can see all results in raw format.
Conclusion
PostgreSQL extension smlar can be used in systems where we need search similar objects, like texts, images, videos.
That’s all folks! Thank you for reading till the end.This is
re-post from my blog.
 Once you have to calculate the intensity of all pixels in a 15×15 matrix, we find the ratio of the intensity of each pixel to the mean intensity of the matrix, and generate a unique number for each cell (in the code to generate unique for each cell, I added the coordinates to intensity) and obtain an array of 225 elements length (15 * 15 = 225). Excellent.
Once you have to calculate the intensity of all pixels in a 15×15 matrix, we find the ratio of the intensity of each pixel to the mean intensity of the matrix, and generate a unique number for each cell (in the code to generate unique for each cell, I added the coordinates to intensity) and obtain an array of 225 elements length (15 * 15 = 225). Excellent. Below is the code to generate a digital signature for images on Ruby and PHP languages:Ruby PHP
Below is the code to generate a digital signature for images on Ruby and PHP languages:Ruby PHP 





